С╗ітцЕтєЇСЙєуюІСИђтЅЄ┬аDerek Muller┬ауџёТЈљтЋЈтй▒уЅЄ
№╝▒№╝џт░ЄТГЦТДЇуй«ТћЙТќ╝ТюетАіуџёТГБСИІТќ╣№╝їуЋХтГљтйѕт░ётЁЦТюетАіжђџжЂјУ│фт┐ЃуџёСИГУ╗ИуиџТЎѓ№╝їтдѓТъютГљтйѕтЪІтЁЦТюетАіСИГУђїТюфТЊіуЕ┐ТюетАі№╝їжѓБж║╝тїЁУЉЌтГљтйѕуџёТюетАіТюЃтЙђСИітйѕУи│С║єТЪљтђІжФўт║дсђѓТјЦУЉЌт░ЄТГЦТДЇтЙђтЈ│Тїф№╝їУ«ЊтГљтйѕт░ёТЊіТюфжђџжЂјУ│фт┐ЃуџёТюетАітЈ│Тќ╣№╝їтЅЇтЙїтЁЕжАєтГљтйѕуџёуЂФУЌЦжЄЈуЏИтљї№╝їУђїуггС║їТгАт░ёТЊітЙїтГљтйѕС╣ЪТюфТЊіуЕ┐ТюетАісђѓућ▒Тќ╝тГљтйѕуџёт░ёТЊіТќ╣тљЉтЂЈжЏбС║єУ│фт┐Ѓ№╝їТЅђС╗ЦТюетАітюетљЉСИітйѕУи│ТЎѓС╣ЪТюЃжђаТѕљТЌІУйЅсђѓУЕдтЋЈуггС║їТгАТюетАітйѕУи│ТЎѓтЁХУ│фт┐ЃТЅђУЃйСИітЇЄуџёТюђтцДжФўт║дТ»ћуггСИђТгАжФўжѓёТў»Сйј№╝Ъ
1. уггС║їТгАУ╝ЃжФў
2. уггС║їТгАУ╝ЃСйј
3. С║їТгАжЃйСИђТеБжФў
СЙєуюІуюІухљТъю№╝џ
жђЎтђІт»джЕЌухљТъюС╝╝С╣јУиїуа┤СИЇт░ЉС║║уџёую╝жЈА№╝їтй▒уЅЄТњГтЄ║тЙїт╝ЋСЙєує▒уЃѕуџёУејУФќ№╝їуЋЎУеђжФўжЂћтЏЏтЇЃтцџтЅЄ№╝їтЁХСИГСИЇС╣Јт»джџЏжЄЇУцЄжђЎтђІт»джЕЌСЙєжЕЌУГЅухљТъюуџёС║║№╝їжѓБж║╝С║їУђЁуџёУ│фт┐ЃСИітЇЄжФўт║дуѓ║С╗ђж║╝ТюЃуЏИтљїтЉб№╝Ъ
УДБТъљ№╝џ
у░Атќ«уџёУфф№╝їућ▒Тќ╝С║їУђЁтЮЄуѓ║┬ат«їтЁежЮътйѕТђДуб░Тњъ№╝їТЅђС╗ЦС║їуе«ТеАт╝ЈуџёУ│фт┐ЃжђЪт║дуЏИтљї№╝їУ│фт┐ЃтІЋУЃйуЏИтљї№╝їтЏаТГцУ│фт┐ЃуѕгтЇЄуџёжФўт║дт░▒уЏИтљїсђѓ
ТѕќУе▒ТюЅС║║ТюЃУфЇуѓ║сђїжђЎТў»С╗ЦтІЋжЄЈуџёУДњт║дСЙєУђЃжЄЈ№╝їжђЎТ▓њтЋЈжАїсђѓСйєТў»УІЦтЙъУЃйжЄЈуџёУДњт║дСЙєТђЮУђЃТЎѓ№╝їуггС║їуе«ТеАт╝ЈуџёуИйтіЏтГИУЃйСИЇт░▒СИЇуГЅТќ╝уггСИђуе«уџёТеАт╝ЈС║є№╝ЪжђЎтђІтцџтЄ║СЙєуџёУйЅтІЋтІЋУЃйТў»Тђјж║╝тЏъС║І№╝ЪсђЇOK№╝їТјЦУЉЌТѕЉтђЉС╗ЦТЋИтГИСЙєтѕєТъљ№╝џ
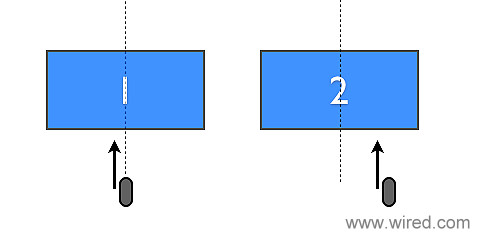
1. УеГТюетАіУ│фжЄЈM┬а№╝їтГљтйѕУ│фжЄЈ┬аm№╝їтГљтйѕт░ётЁЦТюетАітЅЇуџёжђЪујЄуѓ║┬аv№╝їтГљтйѕт░ётЁЦТюетАітЙїуџёУ│фт┐ЃжђЪујЄуѓ║┬аV№╝їтюеуггСИђуе«ТеАт╝ЈСИГ№╝їућ▒Тќ╝┬атІЋжЄЈт«ѕТЂє
уб░ТњътЅЇтГљтйѕтІЋжЄЈ┬аmv┬а= уб░ТњътЙїу│╗ух▒У│фт┐ЃтІЋжЄЈ(M┬а+┬аm)V№╝їтЏаТГц┬аV┬а=┬аmv┬а/ (M┬а+┬аm)сђѓтГљтйѕтѕЮтІЋУЃйуѓ║┬а0.5mv2№╝їт░ётЁЦтЙїу│╗ух▒уџёУ│фт┐ЃтІЋУЃйуѓ║┬а0.5(M┬а+┬аm)V2сђѓтЏаТГцТљЇтц▒уџётІЋУЃй┬а= 0.5mv2┬а– 0.5(M┬а+┬аm)V2┬а┬а=┬а(0.5mv2) [M/(M+m)]№╝їС╣Ът░▒Тў»ТљЇтц▒уџётІЋУЃйСйћС║єтјЪтЁѕтГљтйѕтІЋУЃйуџё [M/(M+m)]тђЇ№╝їтЁХУйЅТЈЏТѕљуѓ║у▓ЅубјТюеТЮљу║ќуХГТЅђтЂџуџётіЪтЈіућбућЪуџёує▒УЃй
2.┬атюеуггС║їуе«ТеАт╝ЈСИГ№╝їтІЋжЄЈжѓёТў»т«ѕТЂє№╝їтЏаТГцС╗ЇуёХ┬аmv┬а=┬а(M┬а+┬аm)V№╝їV┬а=┬аmv┬а/ (M┬а+┬аm)сђѓТјЦУЉЌжѓёУдЂУђЃТЁ«┬аУДњтІЋжЄЈт«ѕТЂє┬ауџёТЃЁТ│Ђ
УеГТюетАіуџёт»гт║дуѓ║┬аL┬а№╝їСИдтЂЄУеГтГљтйѕт░ётЁЦж╗ътЙђтЈ│тЂЈуД╗С║є┬аL/4УиЮжЏб№╝їтЏаТГцуЏИт░ЇТќ╝У│фт┐ЃУђїУеђ№╝їтГљтйѕтЁЦт░ётЅЇуџёУДњтІЋжЄЈуѓ║┬аmvL/4сђѓУІЦуб░ТњъуЎ╝ућЪтЙї№╝їу│╗ух▒уџёТЌІУйЅУДњжђЪујЄуѓ║ ¤Ѕ№╝їТюетАіуџё УйЅтІЋТЁБжЄЈ уѓ║┬аI┬а№╝їтЏаТГцт░ётЁЦтЙїу│╗ух▒ТЋ┤жФћуџёУДњтІЋжЄЈТў»┬аI┬а¤Ѕ┬а+┬аm(L/4)2┬а¤ЅсђѓтдѓТъюТюетАіуџёжФўжЂат░ЈТќ╝т»г№╝їжѓБж║╝ТюетАіуџёУйЅтІЋТЁБжЄЈтЈ»С╗ЦУдќуѓ║жЋиТА┐уџёСЙІтГљ№╝їтЁХу╣ъСИГт┐ЃУ╗ИуџёУйЅтІЋТЁБжЄЈ┬аI┬а=┬аML2/12сђѓТа╣ТЊџтГљтйѕт░ётЁЦтЅЇтЙїуџёУДњтІЋжЄЈт«ѕТЂє№╝їтЈ»тЙЌтЄ║у│╗ух▒ТЌІУйЅуџёУДњжђЪујЄ┬а¤Ѕ┬а= 12mv┬а/ [L(3m┬а+ 4M)]сђѓтЏаТГцу│╗ух▒уџёУйЅтІЋтІЋУЃй┬а=┬а0.5┬аI┬а¤Ѕ2┬а+ 0.5┬аm(L/4)2┬а¤Ѕ2=┬а(0.5mv2) [(12mM+9m2)/(3m+4M)2]№╝їС╣Ът░▒Тў»СйћС║єтјЪтЁѕтГљтйѕтІЋУЃйуџё┬а(12mM+9m2)/(3m+4M)2тђЇсђѓ
жЄЇж╗ъСЙєС║є№╝їжђЎжЃетѕєуџёУйЅтІЋтІЋУЃйтЙътЊфСЙє№╝ЪТЌбуёХтЁЕуе«ТеАт╝ЈуѕгжФўуџёжФўт║дуЏИтљї№╝їжѓБж║╝тЈфтЅЕСИІСИђуе«тЈ»УЃй№╝їжѓБт░▒Тў»тГљтйѕжЉйжђ▓ТюетАітЁДТЅђућбућЪуџёує▒УЃйУ«іт░ЉС║є№╝їС║дтЇ│тГљтйѕт░ётЁЦТюетАітЁДуџёУиЮжЏбТюЃУ«іуЪГ№╝їСЙєуюІСИђСИІтЁЕуе«ТеАт╝Јт░ЇуЁДуџёуЋФжЮб№╝џ
ТюЅУХБуџёТў»№╝їС╗ЦжљхжЄўУЃйТи▒тЁЦтГћТ┤ъуџёТи▒т║дСЙєТИгжЄЈТЎѓ№╝їуггС║їуе«ТеАт╝ЈТ»ћуггСИђуе«уюІУхиСЙєу┤ёуЪГС║є10mmтидтЈ│сђѓСйєТў»С╗ЦXтЁЅТјбТИгТЎѓ№╝їС║їУђЁуџётГљтйѕТи▒тЁЦУиЮжЏбтЇ╗тЈѕти«СИЇтцџ№╝їжђЎСИђж╗ъжђБ┬аDerek Muller┬ажЃйУд║тЙЌУеЮуЋ░сђѓС╗ќтЅЄУДБжЄІУффТюЅ97%уџётГљтйѕтІЋУЃйТљЇтц▒У«іТѕљує▒УЃйУѕЄ1%У«іТѕљУйЅтІЋтІЋУЃй№╝їС╗ќУффжђЎтЈЦУЕ▒ТЄЅТюЅТЅђТюг№╝їС╣Ът░▒Тў»С╗ќТЄЅУЕ▓ТюЅТИгжЄЈТюетАіУѕЄтГљтйѕуџёУ│фжЄЈТЅЇтЙЌС╗ЦУффтЄ║жђЎтЈЦУЕ▒сђѓС╗ќТјЦУЉЌУфф№╝џсђїжђЎ1%уЏИт░ЇТќ╝97%Тў»тЙѕтЙ«т░Јуџё№╝їС╗ЦУЄ┤Тќ╝тЁЕуе«ТеАт╝ЈСИІуџётГљтйѕТи▒тЁЦУиЮжЏбт╣ЙС╣јуЏИтљї(97% vs. 96%)сђЇ№╝їжђЎТеБуџёУДБжЄІтЙѕтљѕуљєсђѓСйєТў»С╗ќтЇ╗Т▓њУффТўјС╗ЦжљхжЄўСЙєт»джџЏТИгжЄЈТЎѓ№╝їС║їуе«ТеАт╝ЈСИІуџёжљхжЄўТјбТИгТи▒т║дуѓ║СйЋТюЅтЙѕТўјжА»уџёти«УиЮ№╝ѕжЂИТЊЄТђДУи│жЂј^^№╝ЅсђѓтЁХт»дуГћТАѕт░▒тюетй▒уЅЄСИГуџё7тѕє16уДњУЎЋ№╝їтЏауѓ║тюеуггС║їуе«ТеАт╝ЈСИГ№╝їућ▒Тќ╝тГљтйѕуџёТЁБТђДТюЃжђаТѕљтЁХтюеТюетАіСИГуџёУ╗їУиАтЉѕуЈЙт╝Дтйб№╝їТЌбуёХжђЎтђІт░ётЁЦтГћТ┤ъТў»тйјТЏ▓уџё№╝їжѓБж║╝Сй┐ућеуГєуЏ┤уџёжљхжЄўСЙєТИгжЄЈТЎѓ№╝їуЋХуёХжЄЈтѕ░У╝ЃуЪГУиЮжЏбТЎѓт░▒ТюЃуб░тБЂУђїуёАТ│ЋУйЅтйју╣╝у║їТи▒тЁЦС║є№╝Ђ